유형 : 이진탐색, BFS

[예제]
3 3
1 2 2
3 1 3
2 3 2
1 3[출력]
31. 풀이
출처 : 패스트캠퍼스 - 알고리즘 / 기술면접 완전 정복 올인원 패키지 Online
** 핵심 아이디어
1. 다리의 개수 M은 최대 100,000이며, 중량 제한 C는 최대 1,000,000,000이다.
- 중량 제한이 값이 크기 때문에 이진 탐색으로 풀 수 있을 것이라 의심
- log나 √로 풀 수 있을 것 같은 생각
- 중량 제한 c를 찾고자 하기 때문에, 찾고자 하는 값을 이진 탐색을 수행
- BFS 이용 : 그래프 간선, 노드가 주어졌을 때 특정 노드에서 다른 노드로 이동이 가능한지 판단
- BFS는 다리(간선)의 개수만큼 수행하기 때문에 시간복잡도는 O(M)이다.
→ 이진탐색 시간복잡도 : O(M*logC), 약 3백만
2. 이진 탐색을 이용해 O(M*logC)에 문제를 해결할 수 있다.
3. 한번의 이동에서 옮길수 있는 물품들의 중량의 최대값을 이진 탐색으로 찾는다.
* 반복적으로 중량을 설정하여 노드 1에서 3으로 이동이 가능한 경우를 찾는다. (시작 노드 : 1, 도착 노드 : 3)
ex. 노드 1~3, (1,2) : 9, (2,3) : 5, (1,3) : 2
① 최대 중량 = 9, 최소 중량 = 2
- 최소 중량으로 결과값을 초기화
- 결과 = 2
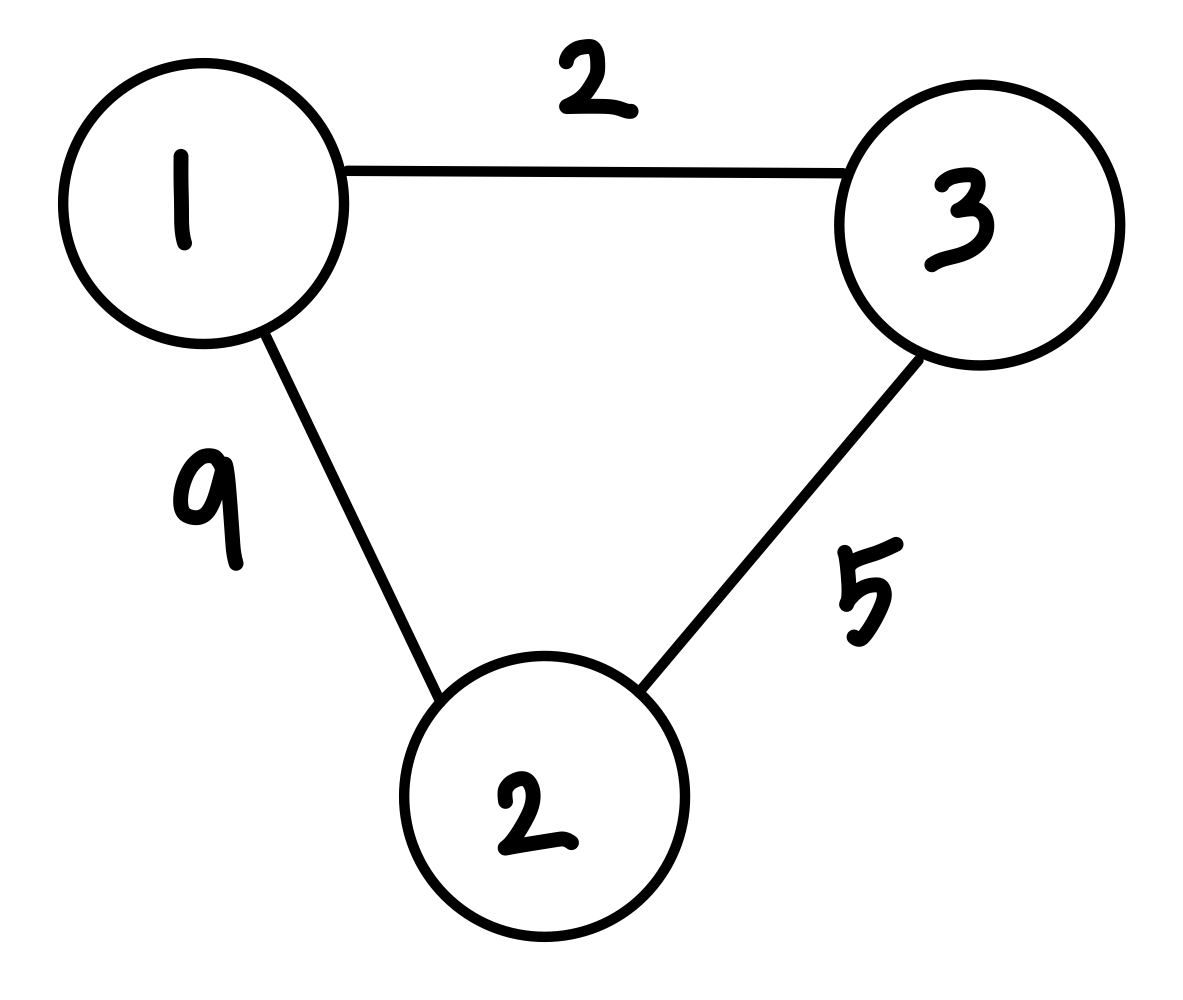
② 최대 중량 = 9, 최소 중량 = 2
- 중량 = 5 ∵ (9+2)//2 = 5
- BFS를 수행해서 중량이 5일 때 이동 가능한지 찾기
- 결과 = 5
→ 이동이 가능하므로, 중량을 증가

③ 최대 중량 = 9, 최소 중량 = 6
- 최소 중량을 현재 중량 + 1로 바꿔줌 ∵ 5+1 = 6
- 중량 = 7 ∵ (9+6)//2 = 7
- 결과 = 5
→ 이동이 불가능하므로, 중량을 감소

④ 최대 중량 = 6, 최소 중량 = 6
- 최대 중량을 현재 중량 - 1로 바꿔줌 ∵ 7-1 = 6
- 중량 = 6
- 결과 = 5
→ 이동이 불가능하며, 더 이상 중량을 감소시킬 수 없음

∴ 결과 = 5
from collections import deque
n,m = map(int, input().split())
adj = [[] for _ in range(n+1)]
## BFS : 경로가 있는지 탐색
def bfs(c):
queue = deque([start_node])
visited = [False] * (n+1)
visited[start_node] = True
while queue:
x = queue.popleft()
for y,weight in adj[x]:
if not visited[y] and weight >= c:
visited[y] = True
queue.append(y)
return visited[end_node]
start = 1000000000
end = 1
for _ in range(m):
x,y,weight = map(int, input().split())
adj[x].append((y, weight))
adj[y].append((x, weight))
start = min(start, weight)
end = max(end, weight)
start_node, end_node = mpa(int, input().split())
## 이진탐색
result = start
while(start <= end):
mid = (start+end)//2 # mid : 현재의 중량
if bfs(mid): # 이동이 가능하므로, 중량을 증가
result = mid
start = mid + 1
else: # 이동이 불가하므로, 중량을 감소
end = mid - 1
print(result)
문제 출처 : https://www.acmicpc.net/problem/1939
1939번: 중량제한
첫째 줄에 N, M(1 ≤ M ≤ 100,000)이 주어진다. 다음 M개의 줄에는 다리에 대한 정보를 나타내는 세 정수 A, B(1 ≤ A, B ≤ N), C(1 ≤ C ≤ 1,000,000,000)가 주어진다. 이는 A번 섬과 B번 섬 사이에 중량제한이
www.acmicpc.net
'Python' 카테고리의 다른 글
| [백준] 1991번 : 트리 순회 ☆ (0) | 2022.01.09 |
|---|---|
| BFS(Breadth-First Search), DFS(Depth-First Search) (0) | 2022.01.05 |
| [백준] 2110번 : 공유기 설치 ☆ (0) | 2022.01.04 |
| [백준] 1236번 : 성 지키기 (0) | 2022.01.04 |
| [백준] 1668번 : 트로피 진열 (0) | 2022.01.03 |




댓글